BUAA-OO-unit1
OO Unit1 Summary
基于度量的代码分析与迭代过程
注:
CogC是认知复杂度,衡量代码的难以理解的程度,CogC说明代码比较难以理解。ev(G)是基本复杂度,衡量非结构化程度,ev(G)高意味着难以模块化和维护。iv(G)是模块设计复杂度,衡量模块的调用关系,iv(G)高意味着模块之间的耦合性高,难以隔离和复用。v(G)是圈复杂度,衡量结构的复杂程度,v(G)是说明代码难以测试和维护。
hw1
重点思路及迭代过程:
- 修改项的定义,实现将表达式分为不剩下符号的一个个项
term——>[+-]{0,2}factor修改定义实现多余符号匹配- 项符号去多余判断符号,累加
- 因子,累乘,最后结果符号设置为项
- 原子组和慵懒防止递归爆炸
- 递归处理表达式因子,正则每次匹配内层,但是有特殊情况如下
((x-1))*((x-1)),判断匹配结果表达式后有*取消计算,防止错误匹配的表达式因子
类图:
PatternString类存储所有需要使用的正则表达式,防止重复声明,Simplify为顶层化简函数,内含有化简表达式、化简项、化简因子的方法逐层递归下降,重新定义项的符号,通过关于term的两个sign方法修复符号,化简通过统一转换为Poly类实现,put方法多态匹配多种待转化字符串或者基础项,通过Tostring输出。
各个类以及代码行数:
主要行数集中在poly和simplify,可见其臃肿。

经典OO度量复杂度分析:
可以看出由于没有将Simplify类较好的分离,复杂度直接爆炸。Poly类也由于多种put方法的存在导致其复杂度较高,其内部有许多高度相似的地方重复定义,可以合并。
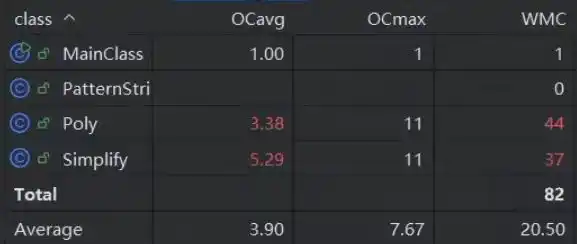
由于使用了正则,需要去掉多余符号和对多层括号的错误匹配进行筛选,因此书写了很多复杂的判断函数,Poly转化字符串的函数也没有分开导致过于复杂。
bug分析:
第一次作业比较简单,通过了全部强测试,唯一遇到的问题就是((x-1))*((x-1))的错误提前化简,需要注意。
对于hack,可以重点从x^0 ,x ^00001 ,x^000,x^10等可能由于直接替换字符串导致的优化问题。
hw2
重点思路及迭代过程:
- sin慵懒匹配防止跨项(或者筛选不含
<>的)- 最外层换为
<>,内层处理完后换成&%,防止匹配过短错误sin^n*cos^mfactor--->(n,m)- 函数递归,先替换后代入子函数
- 将加号后单独化简,再加到表达式后面
x^0输出换为x^z后按顺序换*x^zx^z*x^z- 自定义递推读取
fnf0f1,括号换为[ ]换x/y为a/b后根据映射换位实参,之后递归调用- +后面丢入化简函数,防止四个符号加正数字(或者三个加非数字因子)
- 采用
hashcode区分不同mono,采用递推计算,递推素数取1<<17-1,hashmap转为string- 定义
mono为最小单位:
- 采用
hashcode作为唯一标识,定义为hashmap字符串的hascode
类图:
新增加处理自定义递推函数的Func类和处理三角运算的Mono类,以及正则有关预处理修改定义的方法类Presimp,通过Presimp处理输入为修改后的定义,调用自定义推推函数Func类处理替换得到未化简的式子,调用Simplify化简,Poly中修改为存储Mono项以实现三角因子的存储和运算。
各个类以及代码行数:

经典OO度量复杂度分析:
加入自定义递推函数后,为了处理各种括号的外层替换和换回,新添加了presimp预处理,poly的复杂度有所下降,但是func和presimp依然爆炸。
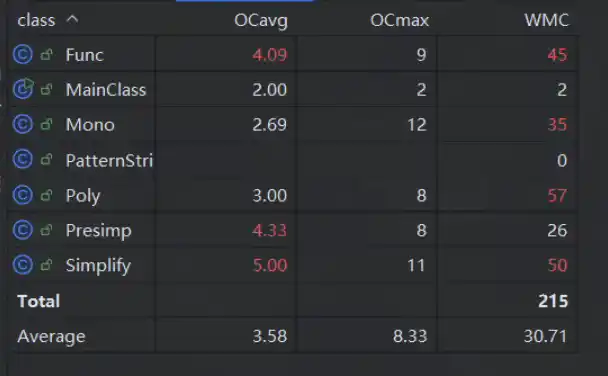
仅仅展示新添的,可以看出Tostring方法过于复杂,原因是中间用了大量分支判断
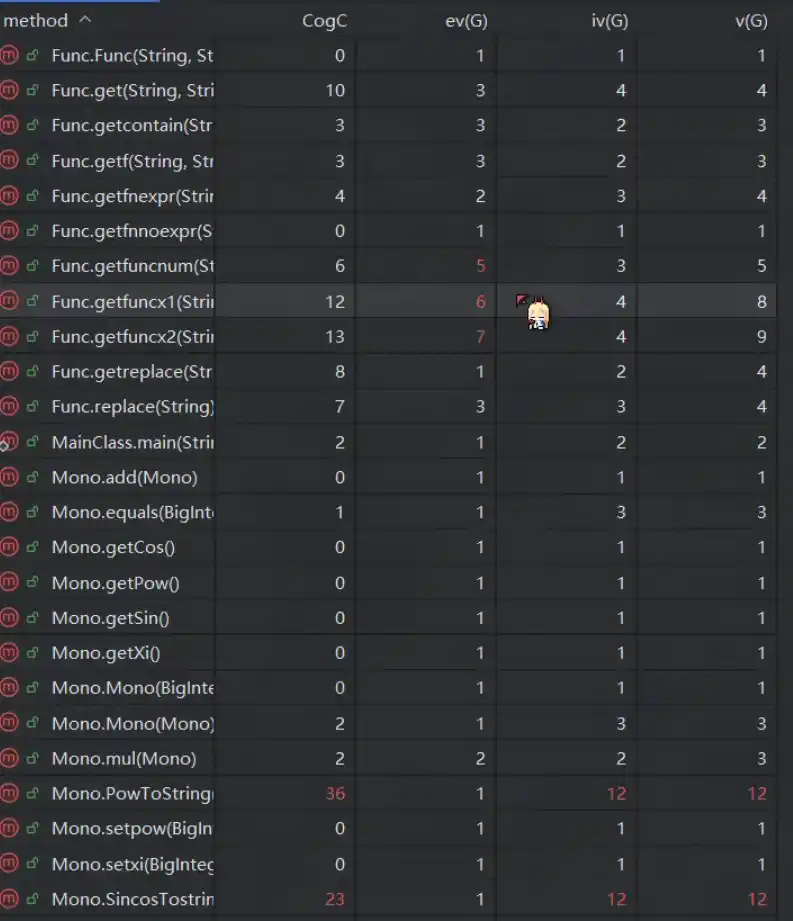
bug分析:
第二次作业为了优化性能问题,采用了hashcode映射sin/cos内部的因子和上方的项组成的hashmap,此处必须使用tostring方法获取hashcode,否则hashmap的hashcode如果不重写,会出现sin(x)*sin(2*x)^2 和 sin(2*x)*sin(x)^2相同的问题。
hack时从多层括号出发重点测试复杂的多余括号,以及自定义递推函数的参数可以多交换测试,尽量保证样例里出现三角、幂次、常数的多种情况,本次一个大坑是fn后的+ 表达式,加号不算作表达式内的符号,如果不做处理, +++ -1 、+ - - x,都会出现问题
hw3
重点思路及迭代过程:
思考化简顺序:
1.easy(input)
换外层括号,循环替换g/h
easy ->替换x,y->easy(contain)->没有g/h返回2.funcreplace
func->替换x,y->替换 “+” 后面的easy(expr)->(simplify(expr))f0 f1替换x,y->替换easy(expr),防止f0 f1 定义里有g/h
3.simplify
dx(k) ->simp4.dx(k)->换最外层dx括号为[ ]
查找替换k含有dx()的因子p为dx(p),循环直到没有dx->没有dx返回原值的导数5.保证expr输入为最简单表达式
dx(expr)-> derive term 链式法则-> derive factor 为poly 乘法法则->poly 中 derive mono返回一个poly6.derive mono
乘法法则,对应sincos内部factor调用 simplify ( “dx( factor )” )
返回值siancos括号换为自定义<>防止polyput不识别
类图:
新添Derivative求导方法类,Func中新添加自定义简单函数化简,实质上是自定义递推函数f0``f1的函数稍微修改。求导方法放入Simplify顶层方法内,调用函数Func类处理自定义递推函数和自定义简单函数,替换得到未化简的式子,调用Simplify化简并且求导,Poly中以Mono为最底层求导因子逐层下降,Mono类实现求导方法,返回一个Poly类(同上机实验的思考),对Mono类的求导只需要操作系数和幂次再乘以因子求导。
各个类以及代码行数:
四大功能的行数最多,代码较为冗杂。

经典OO度量复杂度分析:
不出意外的复杂度爆炸,正则的使用造成了大量处理函数的书写和情况的考虑,造成了不必要的复杂度增长。
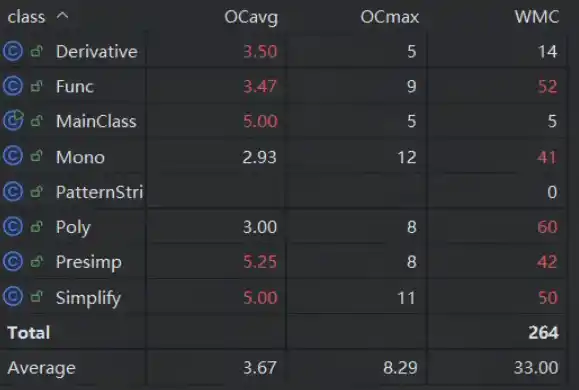
标红的都为为了正则写的处理函数,基本都是面向过程,因此复杂度极高。
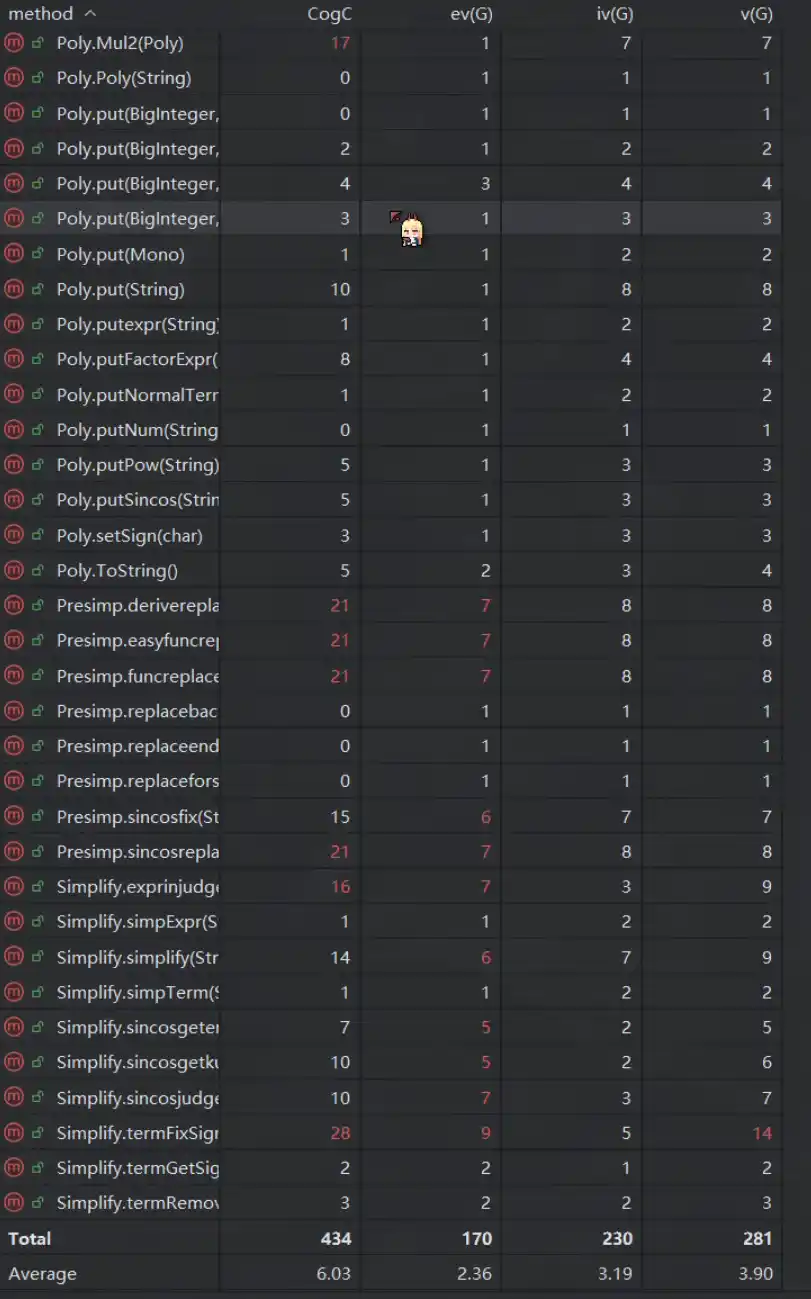
bug分析:
第三次作业迭代开发较为简单,自定义简单函数可以直接套用递推函,这次出错主要问题在于忘记了F0F1中也可能含有自定义简单函数,白白错了很多点,实际上只需要两行就可以修改。
hack时重点放在求导上可能出现的多层函数求导问题,以及递归函数中出现的简单函数的解析(自己就踩了坑),不出所料许多人都犯了这个问题,多层求导关于三角很多人也对内部处理不正确。
心得体会
通过第一单元的训练,我在多个方面都获得了很大的收获:
通过第一次到第二次作业的过渡和遇到的问题,我加深了对正则表达式的理解,学到了慵懒匹配原子组等正则方法,同时用正则遇到的许多问题也使我对多种情况的处理和多层括号的理解进一步加深。
这一单元也遇到了许多问题,第一次作业不知道出于什么心理没有选择普通的递归下降方法,而是采用了正则匹配,这使我相比其他人多考虑了许多情况和多遇到了许多bug,浪费了许多时间,但是当我遇到一个看似不可能解决的多层括号问题,而想出替换括号方法绕开的时候,那种发现新大陆一般的心情也许别人无法感受到。
这次唯一的优点是使用了多态的方法,大大简化了转化POLY的代码结构复杂度,每部分只需要下降到最小因子即可,但是缺点也是代码及其冗长,应该进一步合并重复代码段优化复杂度。
看之前学长的博客,说使用正则会遇到各种各样的问题,作业过程中确实遇到了许多问题(但是也不是完全不能做?),这些问题本身都可以避免,希望在第二单元中可以写出架构更加美观的代码,在第一次作业中就考虑好架构,为之后的作业留下空间,而不是像这次一样打补丁。
还有三个单元,希望自己接下来能够再接再厉
未来建议
个人认为课程组这次的迭代顺序可以略微调整,将自定义简单函数提到自定义递推函数前,这样不仅符合认知,也能更好地锻炼迭代能力,同时优化自定义递推函数后加的表达式,个人认为+ 表达式这种定义除了徒增处理复杂度没有任何意义,如果说考察学生的细节思考能力也完全没有必要从这里入手。
附录
正则匹配的patternstring,留给之后的正则仙人少走一些弯路(虽然正则也算弯路罢了)
修改了项的定义以匹配正确多个符号,修改一些括号以保证只匹配最外层。
1 | import java.util.regex.Pattern; |